前言
现在大部分的边缘计算或者联邦学习的论文,都不免得会提出一个组合优化问题。但是我们现在做的很多组合优化问题都带有复杂的约束。
如果想直接用端到端的深度学习去做,无论是DL还是DRL,和传统的求解器相比,都是既没有办法保证能够得到可行解,也没有办法保证最优解。
提高解的可行性的一个很原始的方法是加惩罚项或者在目标函数上用拉格朗日乘数法。拉格朗日乘数法每有一个约束就要给目标函数加一项,最后一个目标函数有成千上万个项就尴尬了。又或者用更复杂的DRL网络结构(HDRL等),获得更好的性能。但是这和现在的计算机视觉任务或者自然语言处理任务刷分一样,在简单问题上你可能有100%的准确率,但是更复杂的问题又没有办法保证准确率100%,可行性和最优性也一样。
因此现在很多工作都喜欢多次采样取最优值,同时大大提高了可行性,但这也还是原始的做法,没有真正解决约束问题。
Combining Reinforcement Learning and Constraint Programming for Combinatorial Optimization (AAAI2021)
作者提出的是一个RL和Constraint Programming结合的求解组合优化问题的模型,在RL环境和约束规划模型中引入了基于动态规划模型的编码,编码后学习部分用强化学习进行,求解部分用约束规划进行。简单来说是用RL来辅助约束规划在搜索解空间时的分支决策。
为什么可以用动态规划,强化学习应用于组合优化问题是model-base的,既知道状态转移的情况,也知道reward函数。但是我觉得不是deterministic transition的情况下也是可以的,因为现在有很多model free的模型(AC)。
论文正文中给的例子是用RL的结果辅助分支界定法,RL的结果作为新的分支,分支界定法是会舍弃掉不可行解的,所以处理了约束问题。附录中还提到RL与另外两种搜索策略的结合。
和整数规划相比,约束规划可能小众一点,但不一定差,整数规划只能解线性问题和部分非线性问题,但约束规划可以解更general的问题。想讲这篇论文用的强化学习提供搜索heuristic的思路,这个思路是无关CP和MIP的,只是因为论文比较新才选的,因为新的论文,介绍和相关工作里面也能学到更多。
框架:
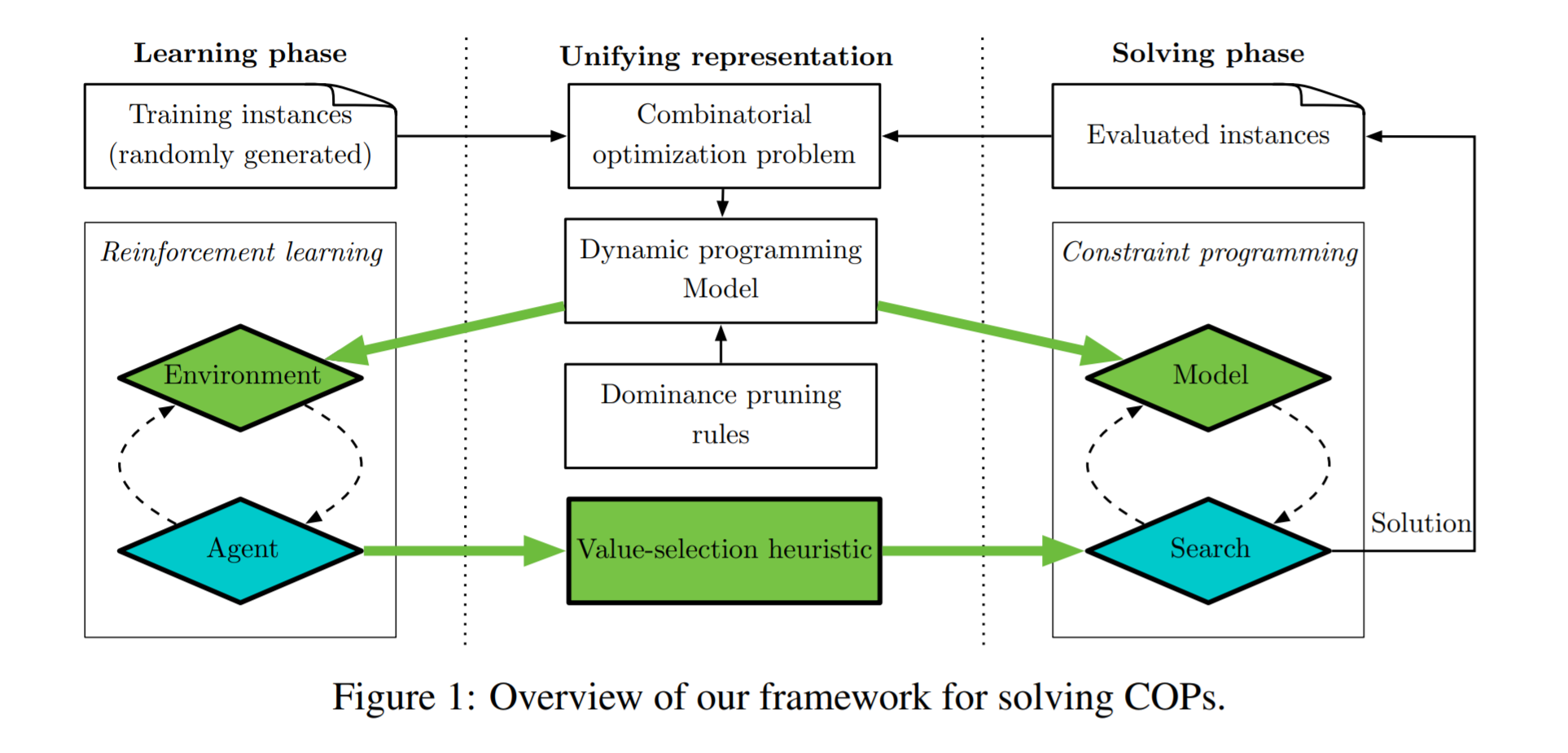
state: 点的特征,比如时间窗和坐标的静态特征,还有和DP相关的动态特征;边的特征,距离;
action: 对应DP的control;
transition: 也是DP的转移;
reward:
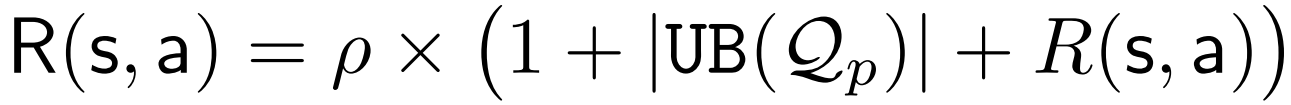
1+UB是一个严格上界,保证reward是正的,避免出现负reward导致提前结束。
DQN辅助分支界定法:

对于有时间窗口约束的旅行商问题,这篇文章是用GAT去编码。最后实验结果比单纯的DRL或者CP要好,与DRL做组合优化的其他文章相比也更好,而且与现行的工业组合优化求解器相比也有优势。
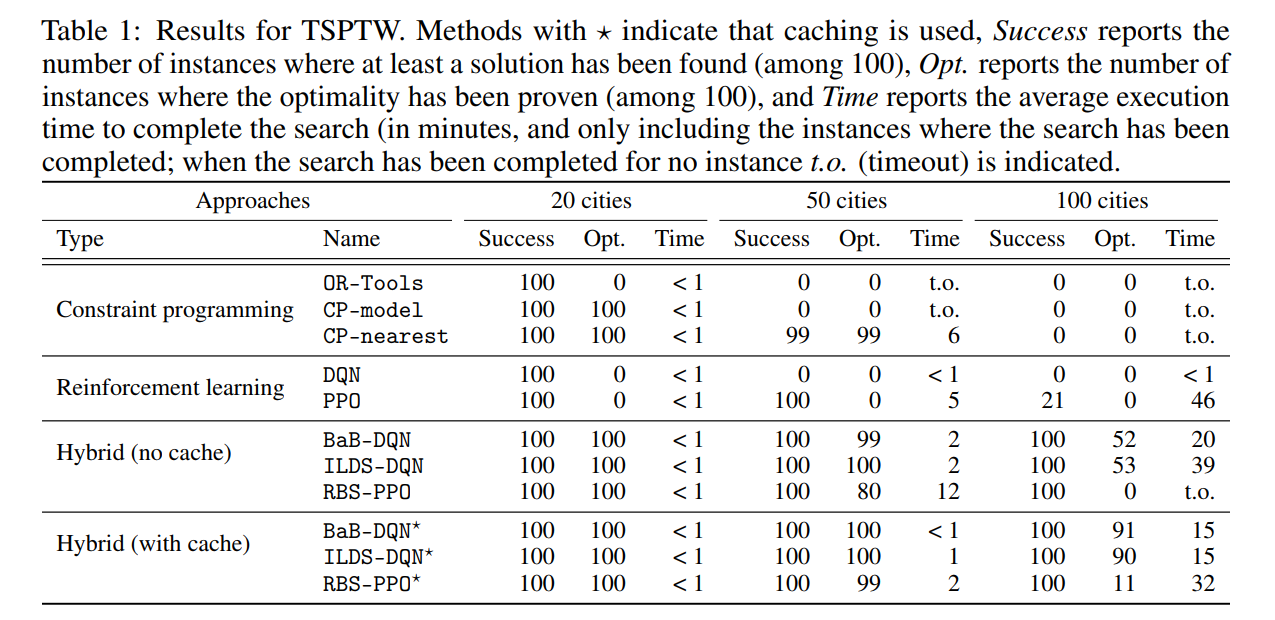
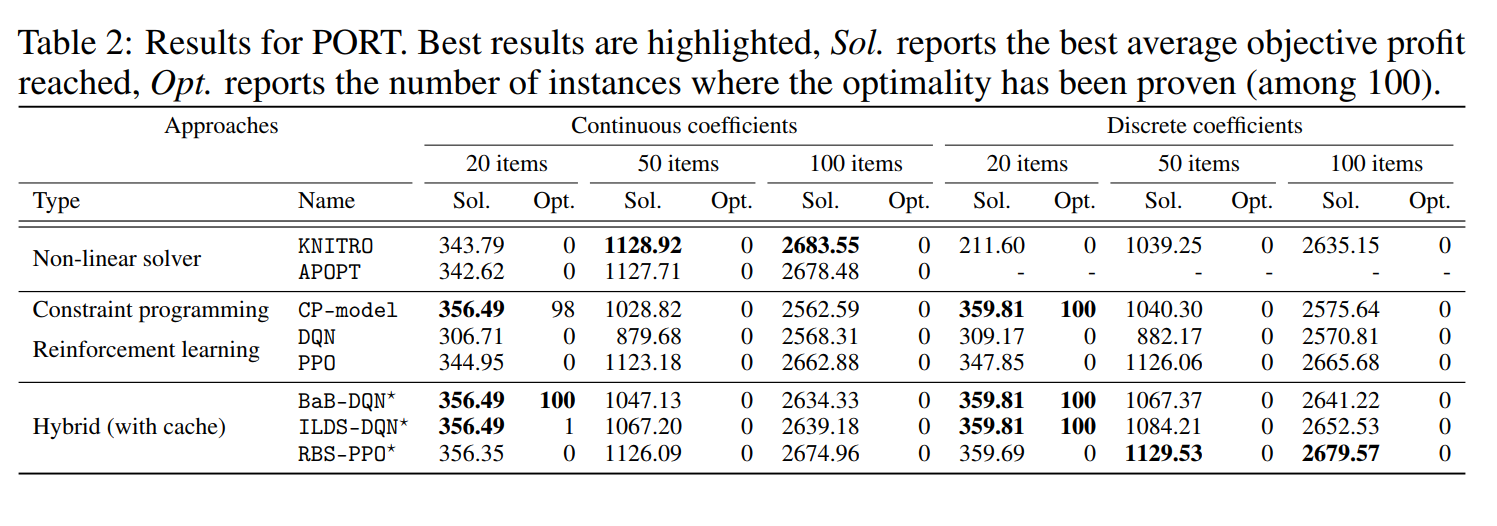
代码写得挺好的,RL和CP的主要结合点在这里,分支定界法取分支的时候,由DQN给出一系列Q值,CP选择最大的那个Q值对应的action,把domain分成采取这个action和采取其他action。

基于这种方法,有人还做了一个叫SeaPearl的CP求解器框架,用强化学习作为value-selection heuristics,用图作为输入
https://github.com/corail-research/SeaPearl.jl
A General VNS heuristic for the traveling salesman problem with time windows
这个应该是SOTA heuristic
前人已经用邻域搜索的方法解决得很好了,能不能强化学习+邻域搜索?
Solving mixed integer programs using neural networks(DeepMind和谷歌Research的团队)
提出了两个组件:Neural Diving和Neural Branching。
Neural Diving是通过深度神经网络生成一个partial assignments,然后交给solver去求解剩下的变量
Neural Branching是通过深度神经网络去模仿学习一个剪枝policy。
最先提出用二部图encode的应该是这篇文章(Exact Combinatorial Optimization with Graph Convolutional Neural Networks)。
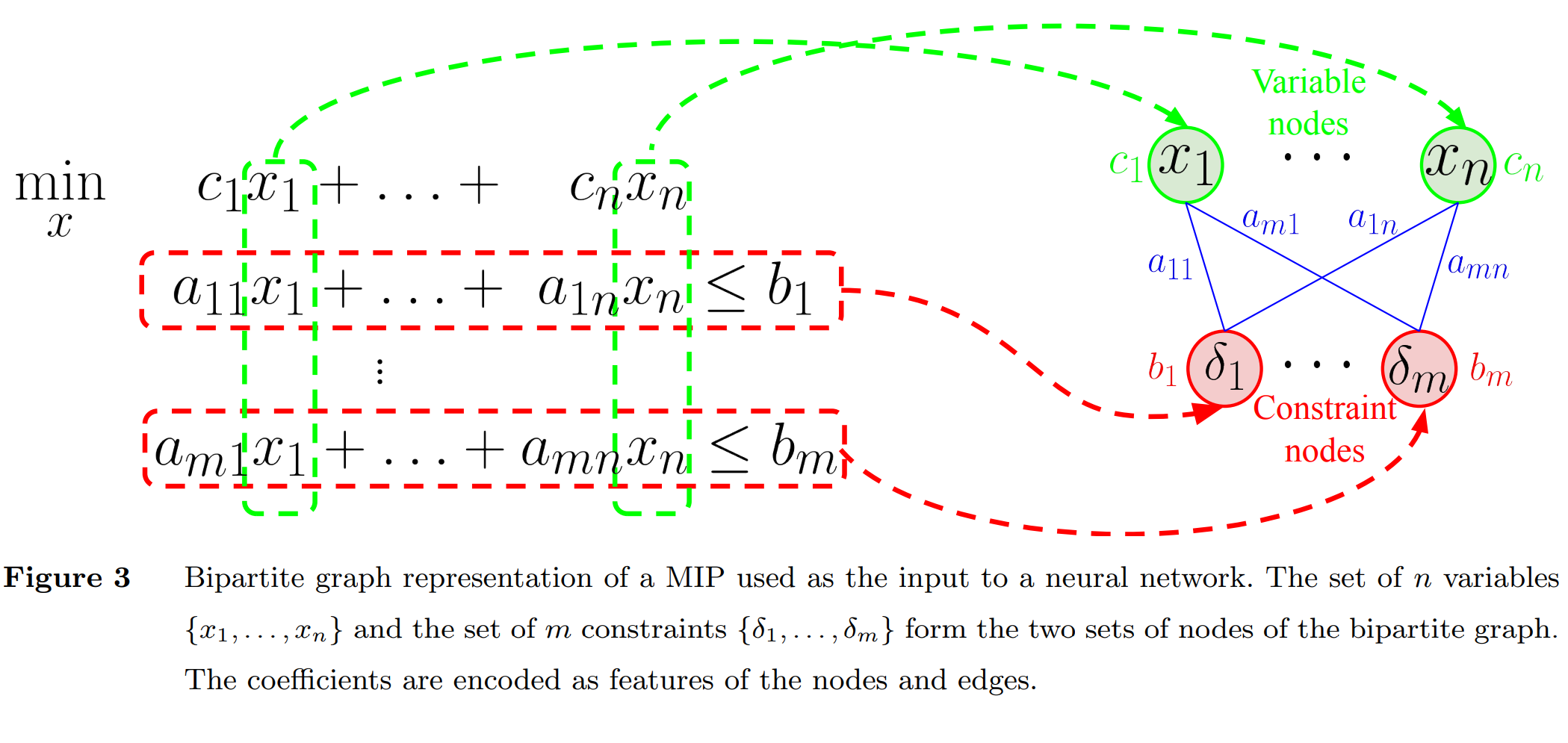
初始特征,有静态特征有动态特征,一般都做一个标准化:
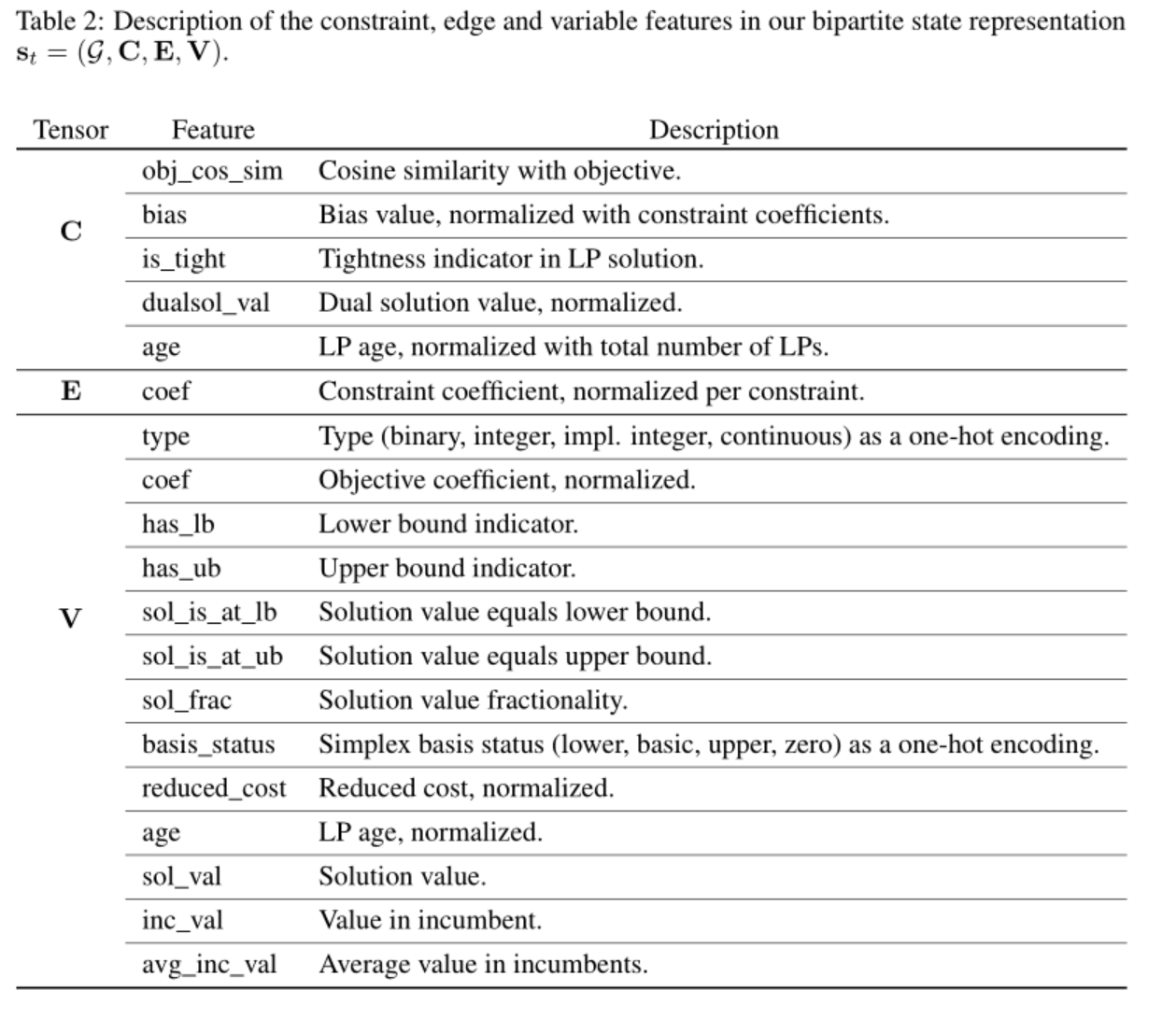
GCN的式子:
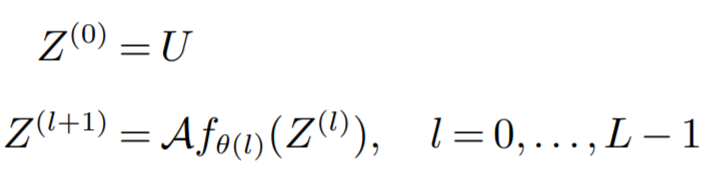
对于二进制变量:
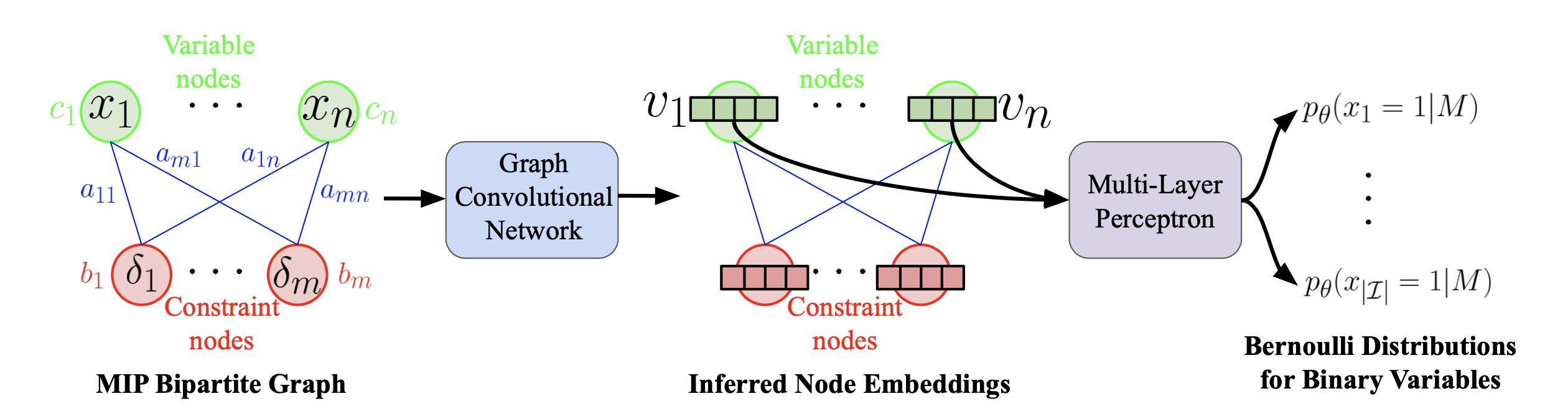
最后的MLP用于所有的v,输出一个概率值。
训练方法:
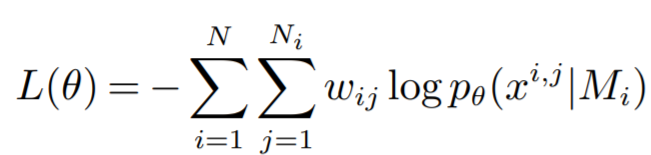
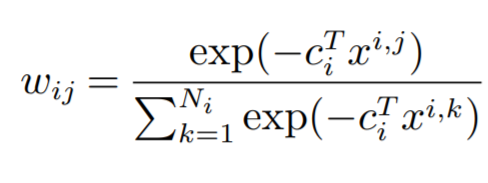
扩展到整数变量:
把整数变量转化为二进制变量来解决,提出可以用二进制序列来表示二分查找的过程。二进制序列代表在二分查找中每次选左边还是选右边。但是因为不知道整数取值范围的基数,可以在训练时先选一个固定基数,如果实际比它大,就只能收紧bound,如果实际比它小,就能得到精确值。

文中没有说网络结构要跟着怎么变,我的理解是对一个v输出多维logits。
Erdos Goes Neural: an Unsupervised Learning Framework for Combinatorial Optimization on Graphs (NeurlPS 2020 oral)
motivation是图神经网络输出的连续值做节点选择的时候,很难做一个二值的操作,容易选到不可行解,而作者提的方法就可以,而且作者提到的方法是无监督的。
作者的损失函数是用概率来表示的,然后给了一个理论保证,在一个可控的概率下面可以可行解和低cost。我的理解是它的图神经网络输出一个概率分布,然后根据这个概率分布算期望cost,然后优化这个cost。
不太能看懂这篇文章,证明和算法交织在一起,也没有伪代码。
作者提出的损失函数是这样的:
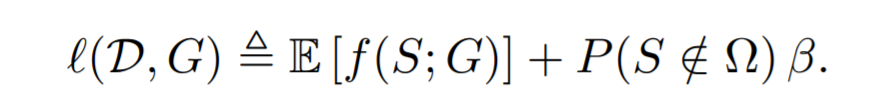
求最大团问题的一个例子:
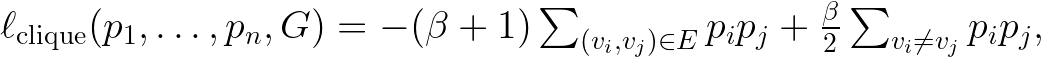
训练好之后有一个采样解的过程,说是用条件概率的方法从高概率到低概率遍历每一个点,不知道为什么可以这样。


然后这篇文章有理论证明只要β满足一些条件,就不会有不可行解。
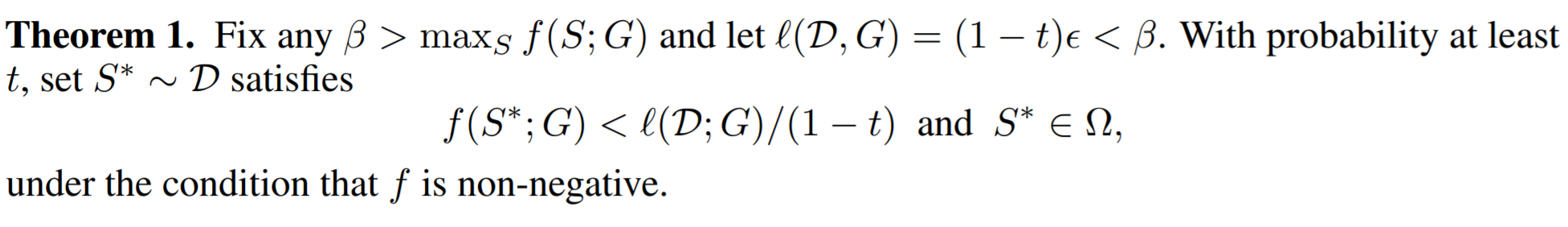
Learning Large Neighborhood Search Policy for Integer Programming (NeurlPS 2021)
文章提出了一种深度强化学习方法来学习整数规划的大邻域搜索(LNS)策略。
heuristics主要分为constructive和improving两种方式,constructive是从头开始构造一个解,improving是不断改进一个解。一般来说constructive在小规模问题上能达到最优,但在大规模问题上improving的最优gap更小。这篇论文是improving的,之前讲的第一篇DRL+CP是constructive的。
这篇论文的特点是它对求解器的侵入性要小很多。
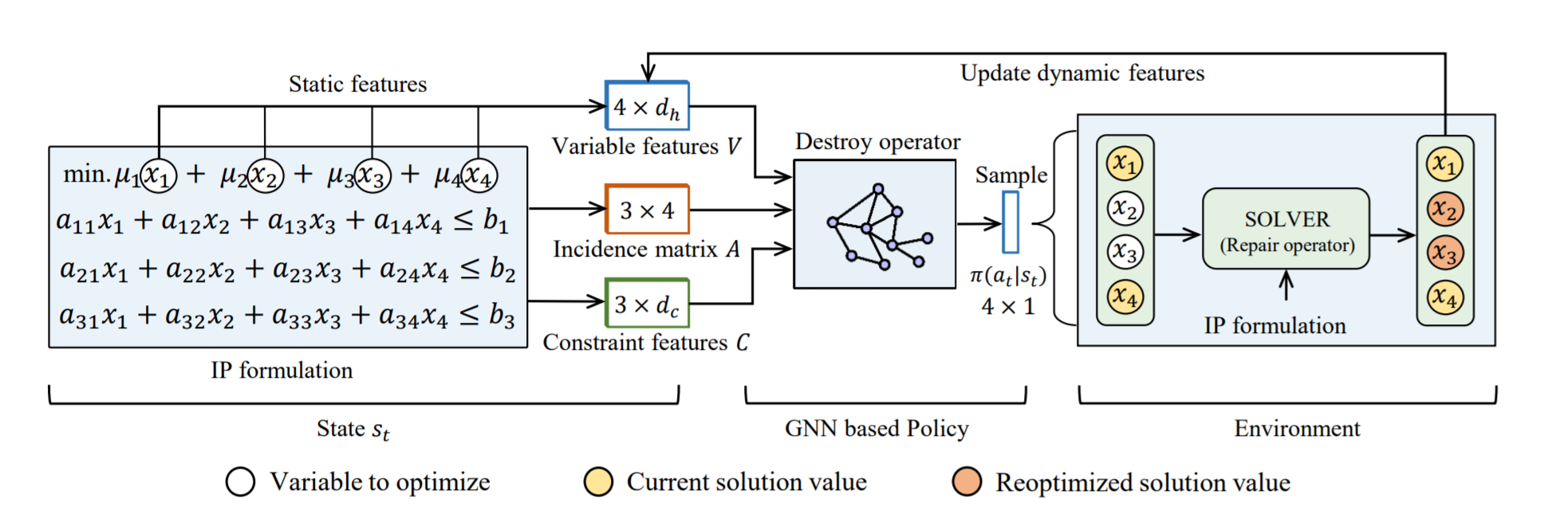

state:既有静态的也有动态的
同样是用了二部图表示,特征:
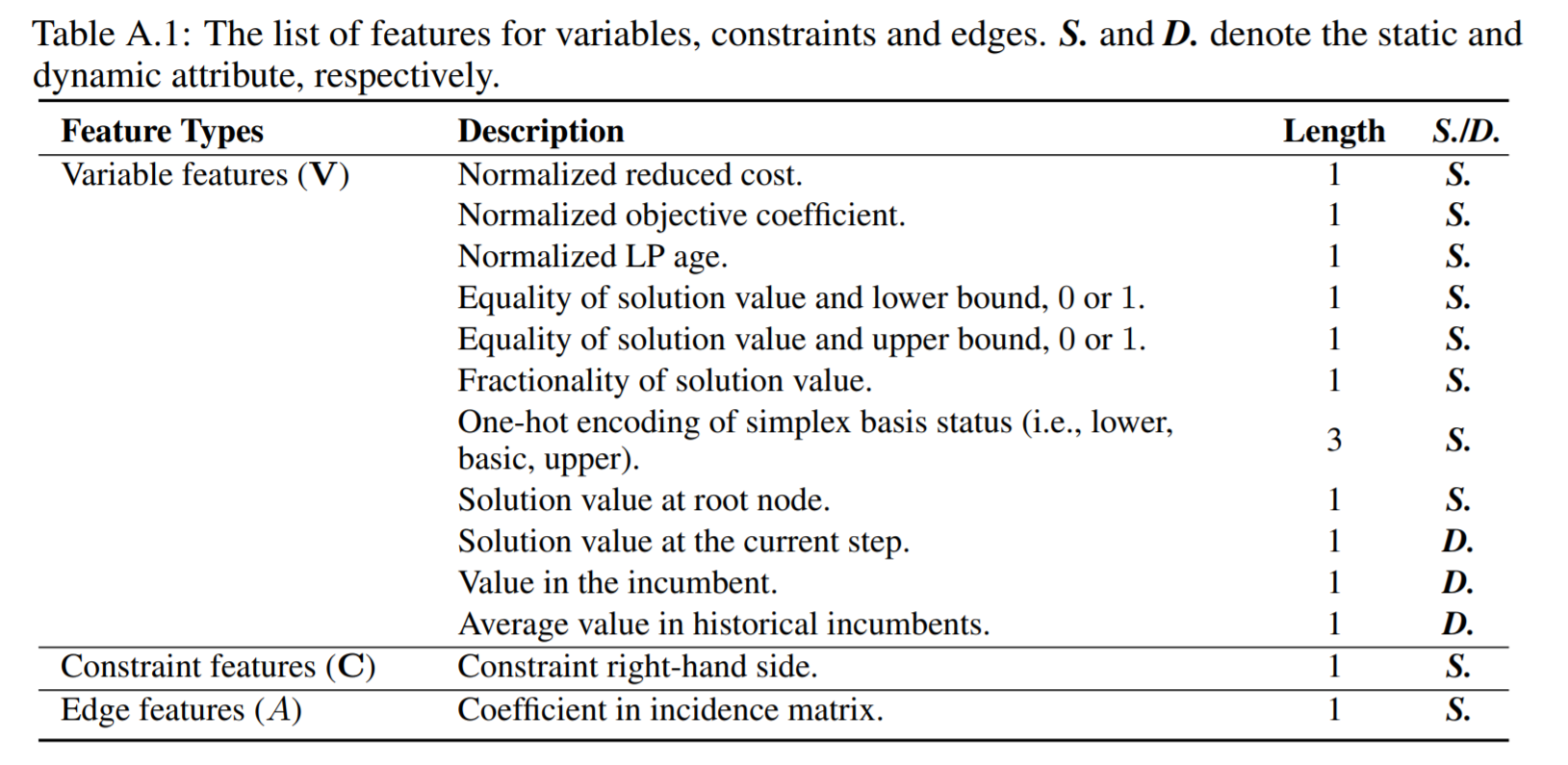
action:选什么subset
transition:solver得到结果后即可得到新状态
rewards: objective value的变化,带discount
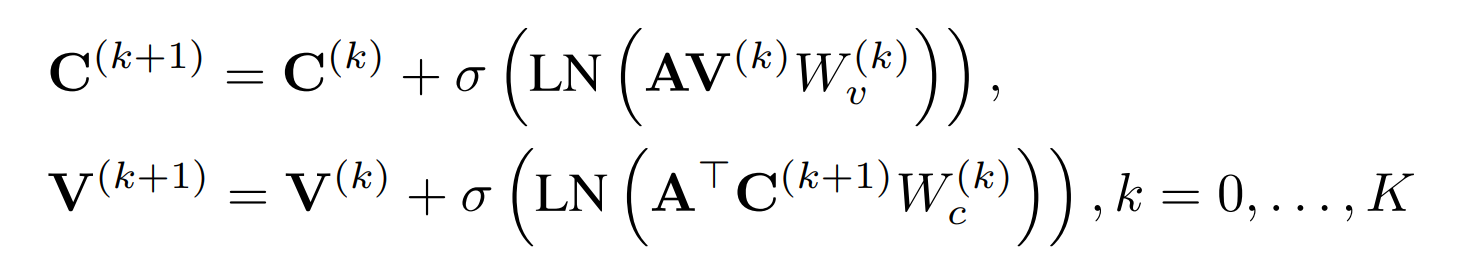
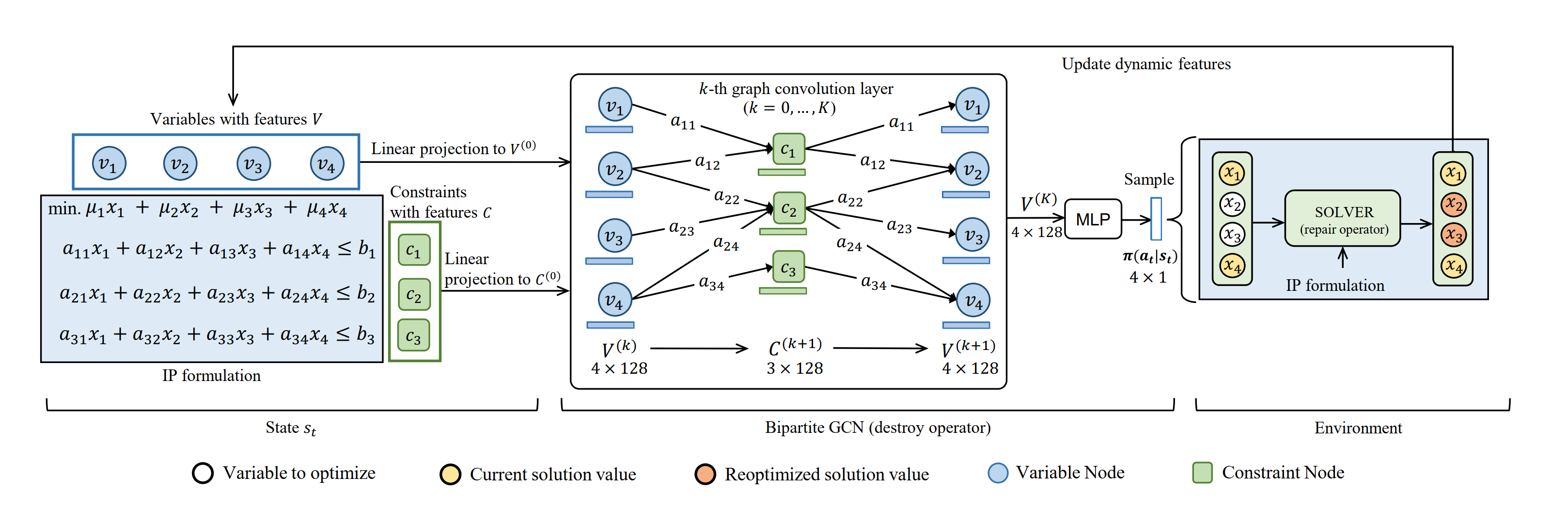
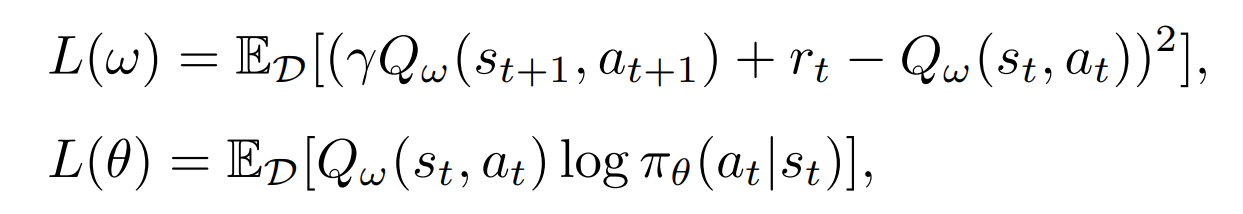
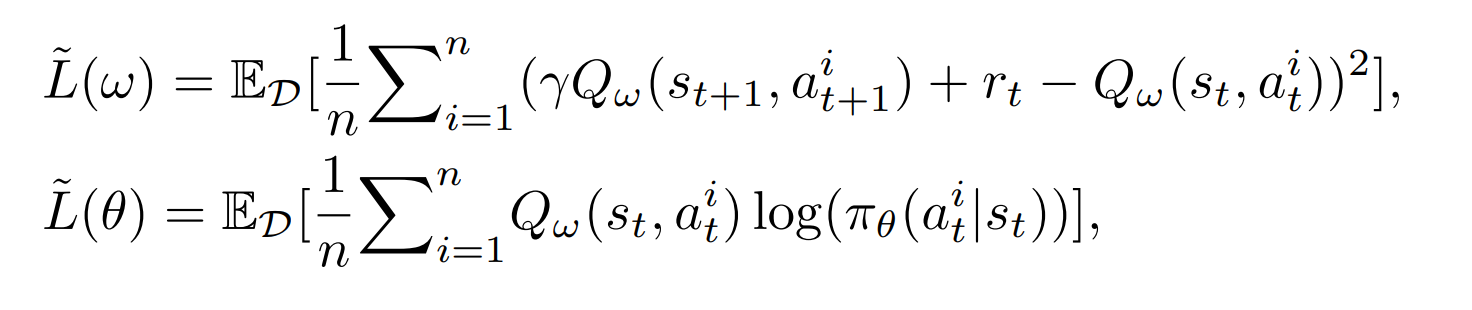
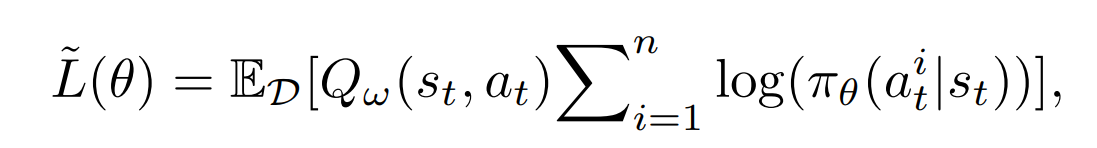
Q的网络结构和actor一样,但是在GCN的输出要加上一维特征表示该节点有没有选,然后用一个MLP做聚合输出最终Q值。
一些细节:为了exploration,actor输出的概率要做一些clipping;空集和全集要重新sample。
创新点是参数共享的GNN,然后对每个节点的值再得出对应policy,这样action space就很小,但是这其实在Solving mixed integer programs using neural networks里面已经提出过类似的了,只不过人家没用DRL。