The model uses embeddings to process sparse features that represent categorical data and a multilayer perceptron (MLP) to process dense features, then interacts these features explicitly using the statistical techniques proposed in the paper of factorization machines. Finally, it finds the event probability by post-processing the interactions with another MLP.

Some known latent factor methods

Matrix Factorization

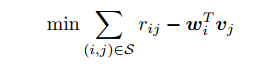
Factorization Machine

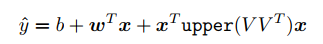
MLP

Architecture

To process the categorical features, each categorical feature will be represented by an embedding vector of the same dimension, generalizing the concept of latent factors used in matrix factorization. To handle the continuous features, the continuous features will be transformed by an MLP (which we call the bottom or dense MLP) which will yield a dense representation of the same length as the embedding vectors.

The model computes second-order interaction of different features explicitly, following the intuition for handling sparse data provided in FMs, optionally passing them through MLPs. This is done by taking the dot product between all pairs of embedding vectors and processed dense features. These dot products are concatenated with the original processed dense features and post-processed with another MLP (the top or output MLP), and fed into a sigmoid function to give a probability.

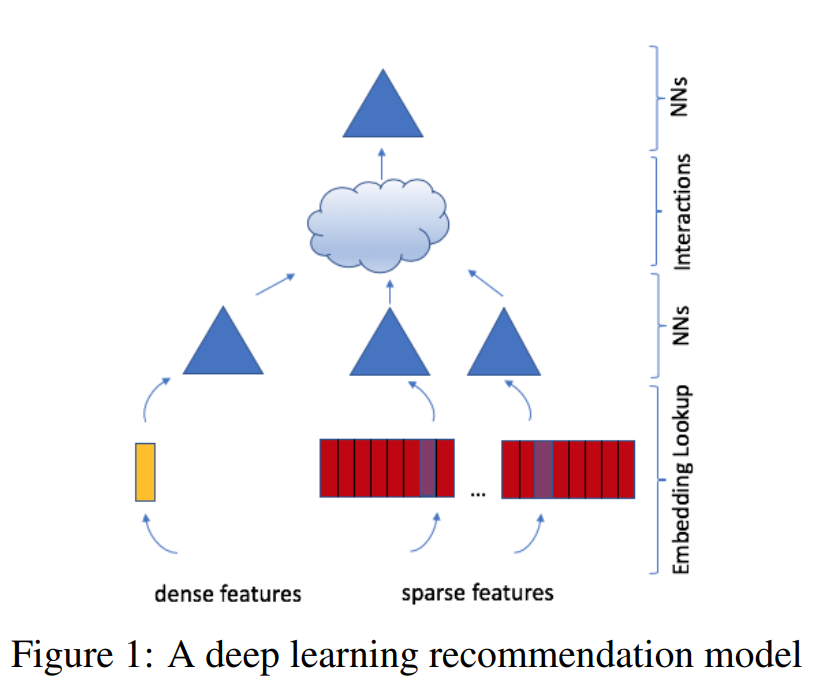
DLRM specifically interacts embeddings in a structured way that mimics factorization machines to significantly reduce the dimensionality of the model by only considering cross-terms produced by the dot-product between pairs of embeddings in the final MLP.

The authors argue that higher-order interactions beyond second-order found in other networks may not necessarily be worth the additional computational/memory cost.

DLRM interprets each feature vector as a single unit representing a single category, resulting in lower dimensionality.

Parallelism

Embeddings contribute the majority of the parameters, with several tables each requiring in excess of multiple GBs of memory, making DLRM memory-capacity and bandwidth intensive. The size of the embeddings makes it prohibitive to use data parallelism since it requires replicating large embeddings on every device. In many cases, this memory constraint necessitates the distribution of the model across multiple devices to be able satisfy memory capacity requirements.

As expected, the majority of time is spent performing embedding lookups and fully connected layers. Running on the CPU, fully connected layers take a significant portion of the computation, while running on the GPU they are almost negligible. I suspected that most of the time are spent on the all-to-all communication.